什么是AVL平衡二叉树，AVL树有哪些特性？

admin linux 2023-01-26 616浏览 0

AVL平衡二叉树

平衡二叉树也叫AVL（发明者名字简写），也属于二叉搜索树的一种，与其不同的是AVL通过机制保证其自身的平衡。

AVL树是最先发明的自平衡二叉查找树。

在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。

增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。

AVL树的特性

AVL树本质上还是一棵二叉搜索树，它有以下特性：

特性1：对于任何一颗子树的root根结点而言，它的左子树任何节点的key一定比root小，而右子树任何节点的key 一定比root大；
特性2：对于AVL树而言，其中任何子树仍然是AVL树；
特性3：每个节点的左右子节点的高度之差的绝对值最多为1；

特性1表明，AVL 继承于 BST , 所以:

1.AVL本身首先是一棵BST 二叉搜索树。
2.AVL带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

在插入、删除树节点的时候，如果破坏了以上的原则，AVL树会自动进行调整使得以上三条原则仍然成立。

也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。

AVL树的平衡功能

举个例子，下左图为AVL树最长的2节点与最短的8节点高度差为1；

当插入一个新的节点后，根据上面第一条原则，它会出现在2节点的左子树，但这样一来就违反了原则3。

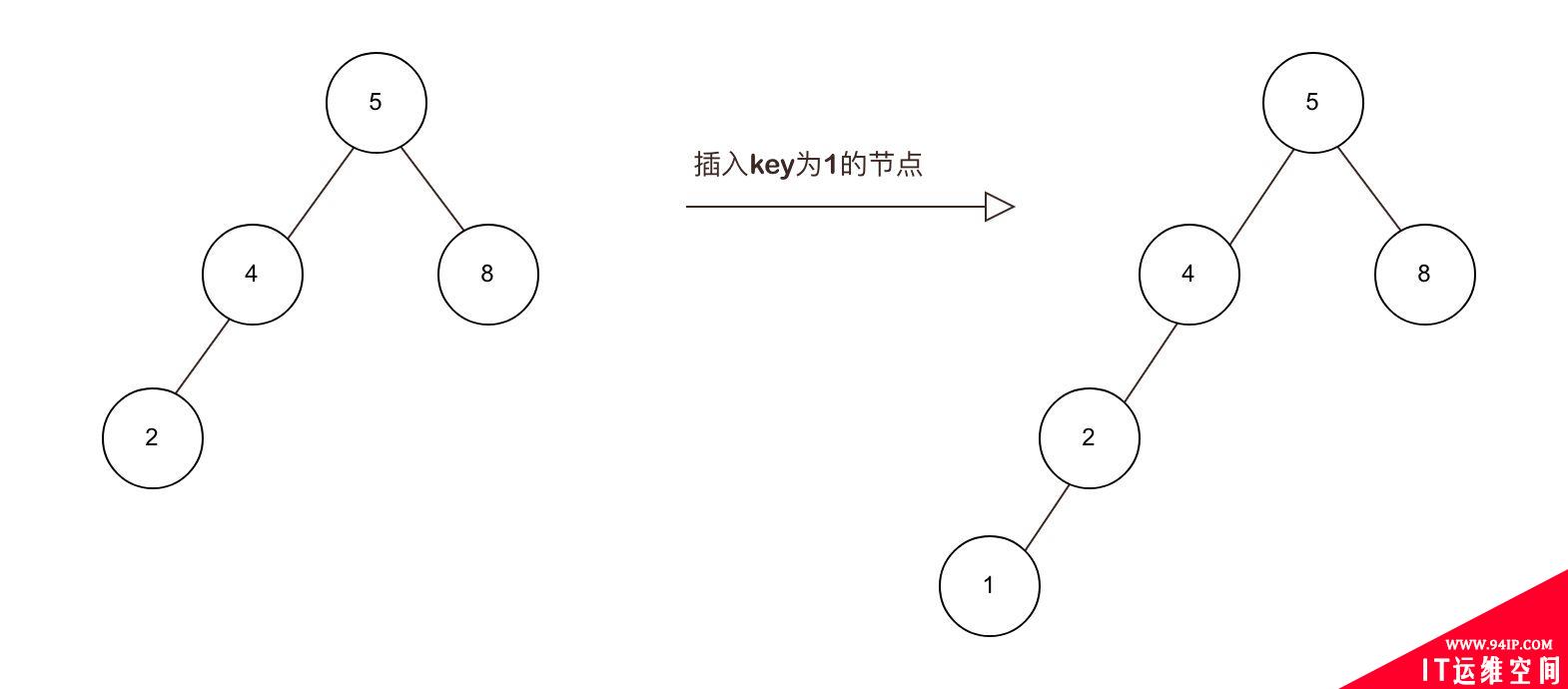
此时AVL树会通过节点的旋转进行进行平衡，

AVL调整的过程称之为左旋和右旋，

AVL平衡的调整过程

旋转之前，首先确定旋转支点（pivot）： 这个旋转支点就是失去平衡这部分树，在自平衡之后的根节点，

平衡的调整过程，需要根据pivot它来进行旋转。

我们在学习AVL树的旋转时，不要将失衡问题扩大到整个树来看，这样会扰乱你的思路，

我们只关注失衡子树的根结点 及它的子节点和孙子节点即可。

事实上，AVL树的旋转，我们权且叫“AVL旋转”是有规律可循的，因为只要聚焦到失衡子树，然后进行左旋、右旋即可。

很多人在左旋和右旋有时候弄不明白，

其实左旋就是逆时针转，右旋是顺时针转

说明：本文会以pdf格式持续更新，更多最新尼恩3高pdf笔记，请从下面的链接获取：语雀或者码云

AVL子树失衡的四大场景

导致AVL失衡的场景就是有限的4个：

左左结构失衡（LL型失衡）
右右结构失衡（RR型失衡）
左右结构失衡（LR型失衡）
右左结构失衡（RL型失衡）

删除元素，也会导致AVL失衡，需要再平衡，但是原理和插入元素是类似的。

这里聚焦介绍插入元素的平衡过程，删除元素，不做介绍。

场景1: LL型失衡-左左结构失衡（右旋）：

场景：插入的元素在子树root的左侧不平衡元素的左侧

此时，以root的左儿为支点，也就是，左侧的不平衡元素为pivot(支点), 进行右旋

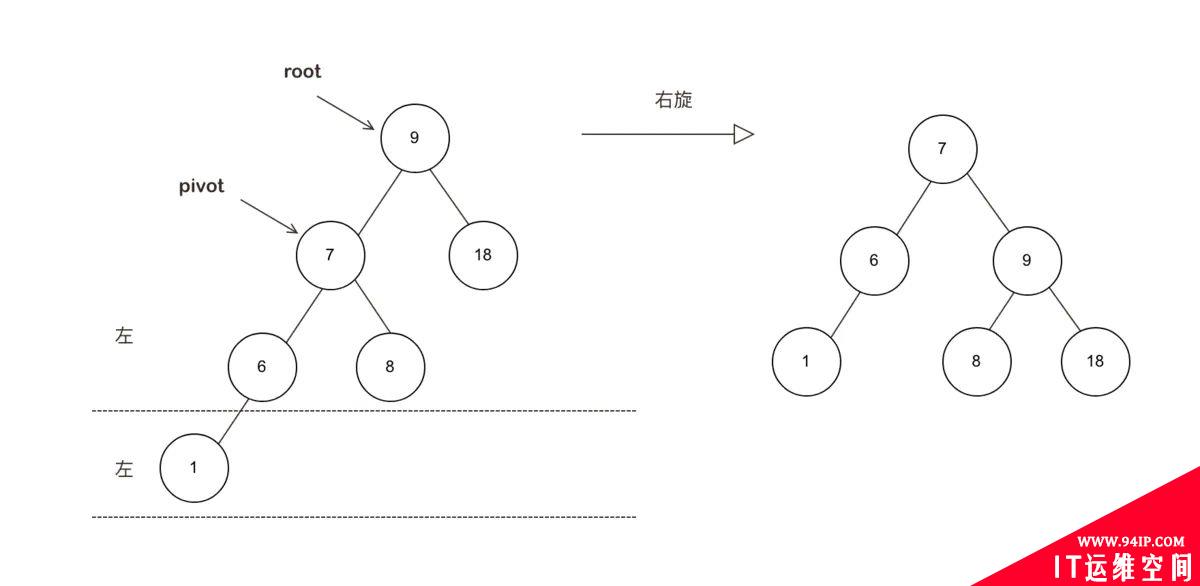
来一个右旋的动画：

右旋过程中，如果pivot有右子树，则作为原root的左子树，保障AVL的特性1

记忆要点

尼恩备注记忆要点，LL型失衡怎么平衡呢？

旋转的反向，与失衡的方向相反，

LL 型失衡，与左边相反的方向，是右边，所以是右旋

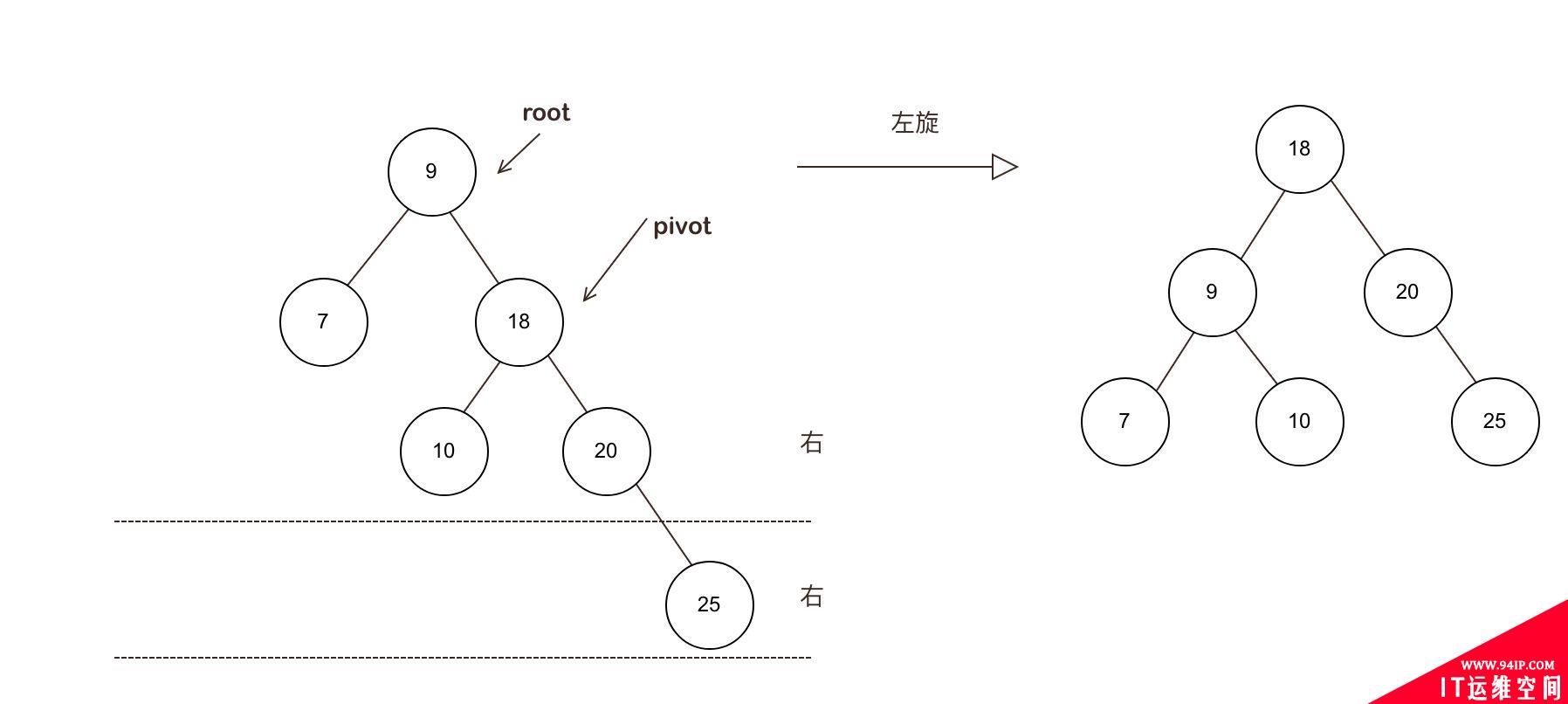
场景2 RR型失衡：右右结构失衡（左旋）

场景：插入的元素在子树root右侧的不平衡子树的右侧

此时，以root的右儿为支点，也就是，右侧的不平衡元素为 pivot(支点)，进行左旋

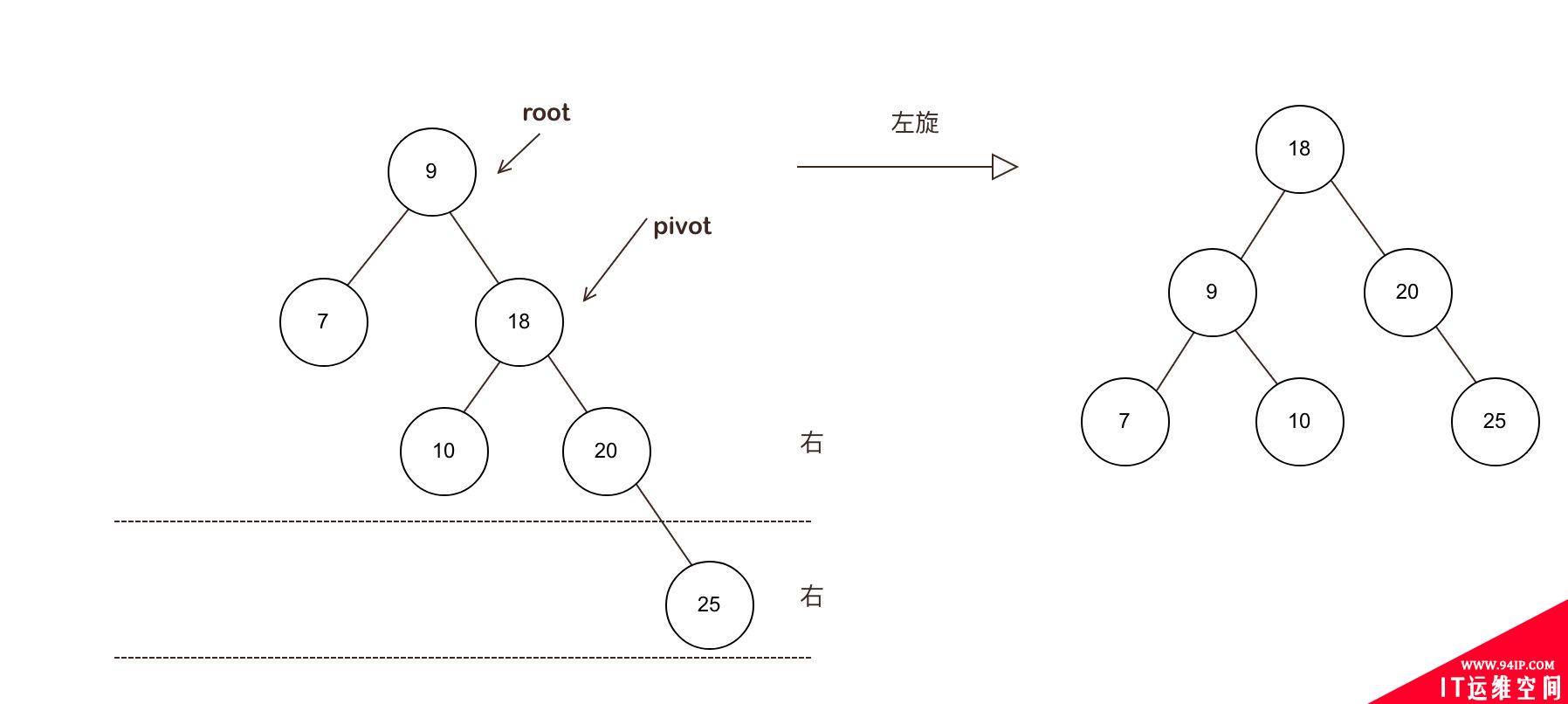
来一个左旋的动画：

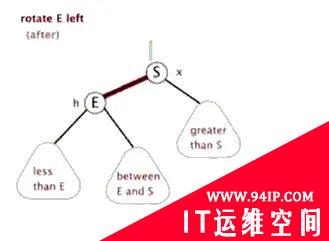
左旋过程中，如果pivot有左子树，则作为原root的右子树，

保障AVL的特性1，

记忆要点

尼恩备注记忆要点，RR型失衡怎么平衡呢？

旋转的反向，与失衡的方向相反，

RR 型失衡，与右边相反的方向，是左边，所以是左旋

场景3 LR型失衡：左右结构失衡（左旋+右旋）：

场景：插入的元素在左侧的不平衡元素的右侧

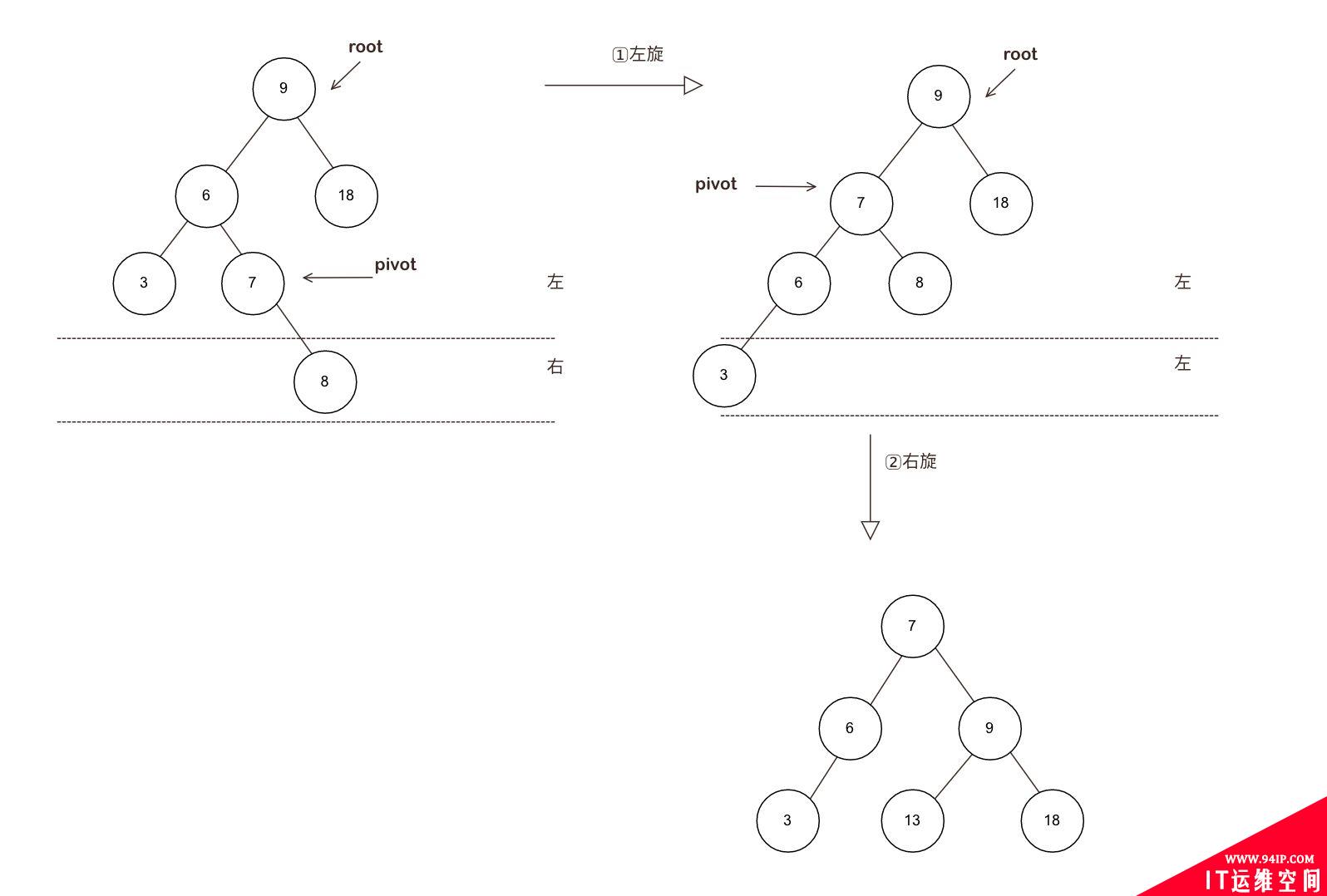
记忆要点

尼恩备注记忆要点，LR型失衡怎么平衡呢？

旋转的反向，与失衡的方向相反，

LR型失衡，与只相反的方向是 RL，但是先旋转底部，再旋转顶部，RL进行次序颠倒，LR

所以， LR型失衡，旋转的方式，是先左旋，再右旋

场景4 RL失衡: 右左结构（右旋+左旋）：

场景：插入的元素在右侧的不平衡元素的左侧

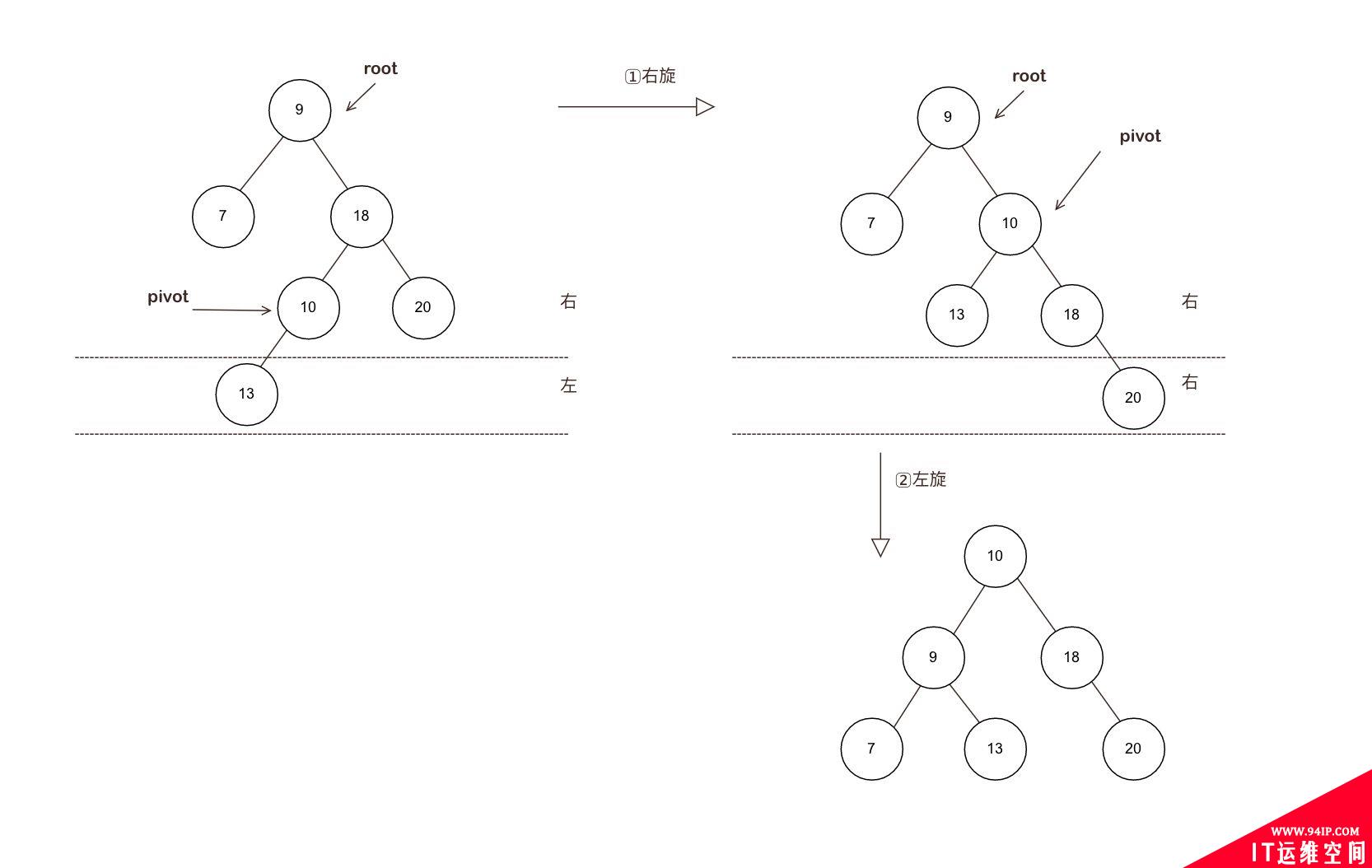
记忆要点

尼恩备注记忆要点，RL型失衡怎么平衡呢？

旋转的反向，与失衡的方向相反，

RL型失衡，与只相反的方向是 LR，但是先旋转底部，再旋转顶部，所以，LR进行次序颠倒，RL

最终， RL型失衡，旋转的方式，是先右旋，再左旋

AVL树平衡总结

可见无论哪种情况的失衡，都可以通过旋转来调整。

不难看出，旋转在图上像是将pivot(支点)节点向上提（将它提升为root节点），而后两边的节点会物理的分布在新root节点的两边，

接下来按照AVL二叉树的要求：

左子树小于root，右子树大于root进行调整。

从图LL结构可以看出，当右旋时原来pivot（7）的右子树（8）会转变到原root点（9）的左子树处；

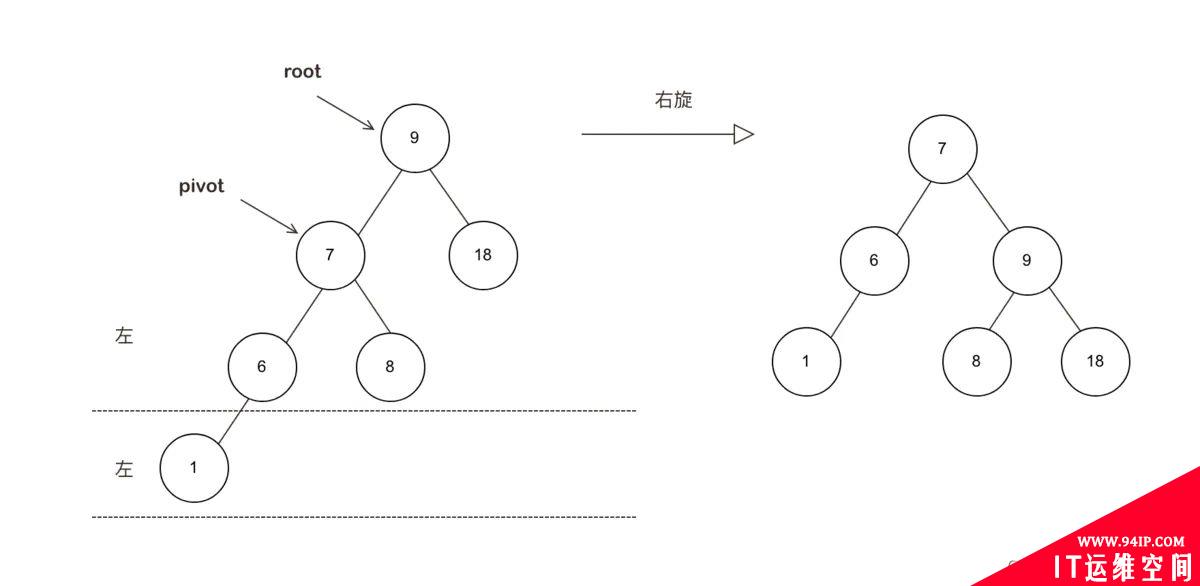
从图右右结构可见，当左旋时，原来pivot（18）的左子树会分布到原root点（9）的右子树。

对于左右结构和右左结构无非是经过多次旋转达到稳定，旋转的方式并没有区别，

AVL树本质上还是一棵二叉搜索树，它有以下特性：
1.本身首先是一棵二叉搜索树。
2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。

AVL树的删除

删除的判断标准

要删除的节点是什么类型的节点？；
删除后是否会破坏平衡；

节点类型

叶子节点；
节点只有左子树或只有右子树；
既有左右子树都有。

处理的思路

当删除为叶子节点，则直接删除，并从父亲节点开始往上看，判断是否失衡；如果没有失衡，再判断父亲的父节点是否失衡，直到根节点。若失衡则判断失衡类型（LL、LR、RR、RL），再进行相应的调整。
删除的节点只有左子树或只有右子树，那么将节点删除，以左子树或右子树进行代替，并进行相应的平衡判断，若失衡则调整，一直到根节点；
删除的节点既有左子树又有右子树，找到其前驱或者后驱节点将其替换，再判断是否失衡，然后根据失衡情况调整，直到根节点。

说明：本文会以pdf格式持续更新，更多最新尼恩3高pdf笔记，请从下面的链接获取：语雀或者码云

常见AVL面试题

问：什么是AVL左旋和右旋？

加入节点后，左旋和右旋，维护AVL平衡性

右旋转

场景：插入的元素在不平衡元素的左侧的左侧

x.right = y

y.left = xxx(原x.right)

   对节点y进行向右旋转操作，返回旋转后新的根节点x
            y                             x
           / \                          /   \
          x   T4     向右旋转 (y)        z     y
         / \       - - - - - - - ->    / \   / \
        z   T3                       T1  T2 T3 T4
       / \
     T1   T2

场景：插入的元素在不平衡元素的右侧的右侧

// 向左旋转过程

x.left = y;

y.right =(原x.left )

对节点y进行向左旋转操作，返回旋转后新的根节点x
        y                             x
      /  \                          /   \
     T1   x      向左旋转 (y)       y     z
         / \   - - - - - - - ->   / \   / \
       T2  z                     T1 T2 T3 T4
          / \
         T3 T4